Controladores do tipo proporcional, integral e derivativo,
comumente chamados de controladores PID podem ser entendidos como sistemas de
controle baseados em resposta a uma equação matemática.
Esses tipos de controladores são os mais populares algoritmos
de controle feedback usados na
indústria. Sendo utilizados em mais da metade dos controladores industriais em
uso atualmente, empregando configurações do controle PID ou PID modificado para
controle de variáveis (pressão, vazão, etc.). (OGATA, 2003, pg. 557)
O funcionamento desses controladores se baseia no cálculo
inicial do erro entre a variável controlada (medida no processo) e seu valor
desejado (set point). O algoritmo PID
usa o erro em três módulos distintos (proporcional, integral e derivativo) para
produzir o sinal de saída de forma a estabilizar e manter estável o sistema da
melhor forma possível.
Em particular, quando o modelo matemático da planta não é
conhecido e, portanto, métodos de projeto analítico não podem ser utilizados,
controles PID se mostram os mais úteis. (OGATA, 2003, pg. 557)
Na área dos sistemas de controle de processos, as
configurações básicas de controle PID e os PID modificados provaram sua
utilidade conferindo um controle satisfatório.
Apesar de se ter a
disponibilidade das ações destes três módulos, em muitas aplicações industriais
não se faz necessária à utilização de um ou mais destes parâmetros. Assim, é
bastante comum encontrar os seguintes tipos de controladores:
- Controlador Proporcional (P);
- Controlador Proporcional e Integral (PI);
- Controlador Proporcional e Derivativo (PD);
- Controlador Proporcional, Integral e Derivativo
(PID);
1.1 Controlador proporcional (P)
Nesse tipo de controlador a ação de
controle, ou seja, a saída do controlador é diretamente proporcional ao erro atuante
oriundo do elemento de medição. Sua saída depende apenas da amplitude do erro
num instante de tempo, sendo o controlador simplesmente um amplificador com um
ganho constante, onde um grande erro em algum instante de tempo acarreta um
valor alto na saída do controlador nesse instante de tempo. (CAMPOS, 2010, pg
25)
O
algoritmo de posição do sinal de saída do controlador P (u(t)) mediante ao erro
(e(t)) atuante, é dado por.
Onde Kp é uma constante, comumente chamada de ganho proporcional do controlador,
definindo esta o quanto a variável de controle deve variar em correspondência a
uma variação unitária do sinal de erro.
Sendo sua função de transferência escrita como:
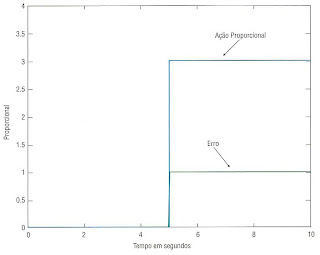
A figura 01 ilustra a ação do controlador proporcional para
um erro em forma de degrau, onde o mesmo apresenta a mesma dinâmica que o sinal
do erro (um degrau), sendo sua magnitude diretamente proporcional ao erro
multiplicado pelo fator Kp (que neste caso é 3). Dessa forma se o erro não
variar a saída do controlador também não irá variar, permitindo um erro em
regime permanente.
Figura 01-Ação proporcional
mediante ao erro em forma de degrau
Fonte: CAMPOS. 2010. pg. 25.
A figura 02 ilustra a resposta de um sistema sob aplicação de
ação proporcional. Sendo quanto maior o ganho Kp, menor o erro em regime permanente, entretanto nunca será
possível anular completamente o erro. Por outro lado, quanto maior o ganho,
mais oscilatório tente a ficar o comportamento transitório do sistema em malha
fechada, ou seja, o aumento excessivo do ganho proporcional pode levar o
sistema à instabilidade.
Figura 02-Saídas de sistema
com controle proporcional, para Kp=1(contínuo), Kp=2(tracejado) e
Kp=4(pontilhado)
Fonte: JUNIOR. 2000. pg.
15
Uma desvantagem do controlador proporcional é sua
incapacidade, em geral, de eliminar erros estacionários, que surgem após uma
mudança de set point ou uma perturbação
constante na saída. (OGATA, 2003, pg. 230)
A figura 03 ilustra a resposta de um controlador proporcional
no qual possui o erro em regime permanente (offset).
Figura 03-Erro de offset
causado após uma mudança de setpoint
Fonte: CRUZ. 2004. pg.
46
Em diversas aplicações de controle em que offsets podem
ser tolerados, o controle proporcional é o mais atraente, sendo justificado por
apresentar grande simplicidade.
Um exemplo pode ser dado para alguns problemas de controle de
nível, onde a manutenção do nível de líquido exatamente no valor do set
point não é necessária, uma vez que basta que o
líquido não extravase ou que o tanque se esvazie por completo.
Em muitos controladores industriais (em especial os modelos
mais antigos) especifica-se o valor percentual da banda proporcional (Pb), ao
invés do ganho proporcional (Kp).
A banda proporcional equivale ao erro que provoca uma variação de 100% na saída
do controlador. Ou seja, é a percentagem do range do
instrumento que corresponde ao curso completo do elemento final de controle. (CAMPOS, 2010, pg 24)
A relação entre a banda proporcional e a constante
proporcional é dada por:
|
A figura 04 ilustra a relação entre o sinal de erro e a ação
de controle gerada pelo modo de controle proporcional, sendo visto a banda
proporcional mediante ao ganho do controlador, constatando que quanto maior KP menor será a banda
proporcional.
Fonte: NOVUS. 2003. pg
04
Um exemplo de aplicação da
banda proporcional seria se em uma válvula de controle, onde Pb fosse 20%. Isso
significaria que uma variação de 20% no erro produzirá uma variação de 100% na
saída, ou seja, a válvula se moverá de totalmente aberta para totalmente
fechada ou vice versa.
Sendo que
se Pb for maior que 100%, não ocorrerá o curso completo da válvula de controle.
Na figura 05 pode ser visualizada a ação da banda
proporcional mediante a resposta de um sistema. Em (A) tem-se um sistema com
grande banda proporcional, acarretando em um alto erro de regime. Em (B) temos
uma banda proporcional de valor ótimo, com um pequeno erro de regime e sem
oscilações. Em (C) a banda proporcional é muito pequena, onde provoca
oscilações no sistema.
Figura
05 – Resposta de um sistema para três valores de PB
Fonte: NOVUS. 2003. pg
03
1.2 Controlador proporcional e integral (PI)
Neste tipo de controlador tem-se a
ação conjunta de dois tipos de controle. O modo proporcional e o integral.
A ação integral ocasiona uma correção tal que sua velocidade
é proporcional à amplitude do desvio. Resumidamente pode-se dizer que a
intervalos regulares, a ação integral corrige o valor da variável manipulada
(MV), somando a esta o valor do desvio (erro). (CAMPOS, 2010, pg 26)
A resposta da ação integral é dada
como sendo proporcional à integral do sinal de erro ao longo do tempo.
A saída do controle integral é dada pelo algoritmo.
Onde Ti é
chamado de tempo integral ou tempo de reset
ou ainda conhecida por controle de reset, tendo este
dimensão de tempo (normalmente em minutos). Sendo nos controladores comerciais
um parâmetro ajustável.
O controle integral raramente é utilizado sozinho, pois tende
a piorar a estabilidade do sistema uma vez que, para que a variável de controle
atinja um valor significativo, é preciso que o erro persista por certo tempo. Por
outro lado, o controle proporcional atua simultaneamente com a ocorrência de um
erro, ou seja, o controlador proporcional toma uma ação corretiva tão logo um
erro seja detectado. Por esta razão, o controle integral é normalmente
utilizado em conjunto com o controle proporcional, constituindo esta combinação
o controlador proporcional integral (PI). (CAMPOS, 2010, pg 28)
Sendo a equação do algoritmo de
posição deste controlador dada por:
Sabendo que 1/Ti é uma
constante de ajustagem (ganho integral) ou número de repetições por segundo.
Representando o número de vezes por unidade de tempo que a parte da ação
proporcional da ação de controle é duplicada.
Ou, equivalentemente, em termos de sua função de
transferência.
A figura 06 ilustra a ação de um controlador integral (I) e
proporcional integral (PI) em relação a um erro em forma de degrau. Onde a ação
integral isolada aumenta ou diminui a saída do controlador indefinidamente
enquanto houver erro. Já a ação do controlador PI cuja ação proporcional
(supondo Kp=3) muda instantaneamente a saída na ocorrência do erro, e a ação
integral continua mudando esta saída enquanto existir o erro. Ficando evidente
que após o tempo integral (2 segundos) a ação integral repete a ação proporcional.
Isto é, ocorrendo o erro de 1%, a saída do controlador será 3% devido à ação
proporcional, e após o tempo integral (2 segundos) a saída é 6% devido à ação
integral de 3% somada á ação proporcional, que continua em 3%.
Figura 06-Sinal de saída de um
controlador com ação proporcional e integral
Fonte: CAMPOS. 2010. pg. 28
Na figura 07 é ilustrada a influência da sintonia do
parâmetro Ti na resposta do sistema proporcional e integral, considerando-se o
sistema com KP=1, e Ti em
2 segundos para a linha pontilhada, 4 segundos para a tracejada e 10 segundos a
continua.
Figure 07-Saída com ação PI: Para KP=1; Ti=2(pontilhado), Ti=4(tracejado) e
Ti=10(contínuo)
Fonte: JUNIOR. 2000. pg.
16
Uma desvantagem do uso da ação integral é que ela tende a
produzir respostas oscilatórias e, portanto, reduzir a estabilidade do sistema.
Uma pequena oscilação normalmente é tolerada, uma vez que isto está em geral
associado com uma rápida resposta. (CAMPOS, 2010, pg 28)
Os efeitos indesejáveis da ação integral podem ser reduzidos
por meio da sintonia apropriada do controlador ou incluindo a ação derivativa,
que tende a compensar os efeitos desestabilizastes.
1.3 Controlador proporcional e derivativo (PD)
Este controlador é resultado da
associação entre o controlador proporcional e o derivativo.
A ação derivativa tem o efeito de reduzir a velocidade das
variações da variável do processo (PV), evitando que se eleve ou reduza muito
rapidamente durante perturbações ou na partida do processo. Sempre atua no
sentido de atenuar as variações, reagindo antecipadamente ao comportamento
futuro do sinal de erro com base na sua taxa de variação (caráter
antecipatório), tendo como principal função melhorar o desempenho do processo
durante os transitórios. (CAMPOS, 2010, pg 30)
O algoritmo de saída do controlador derivativo é expresso
como:
Onde Td é
chamado de tempo derivativo e tem dimensão de tempo (normalmente minutos).
Representando o avanço introduzido pela ação derivativa. Dotando o controlador
de uma capacidade de se antecipar à ocorrência do erro futuro.
Dessa maneira, o avanço
produzido pelo termo derivativo pode compensar o atraso introduzido por
praticamente todas as malhas de controle.
A função de transferência
desta ação é dada por:
A ação derivativa nunca é utilizada sozinha, pois se o erro
fosse constante, o valor do controle seria nulo. Então, sempre é usada em
conjunto com um controlador proporcional que resulta no controlador PD, cujo
algoritmo é dado por. (OGATA, 2003, pg. 234)
Sendo sua
função de transferência:
A figura 08 ilustra a ação de um controlador derivativo (D) e
proporcional derivativo (PD) em relação a um erro em formato de rampa. Sendo
que a ação do controlador puramente derivativo é um valor constante e em forma
de degrau, que no inicio do erro (tempo zero) inicia-se em 15% . Já no
controlador PD o tempo derivativo (Td = 5) antecipa a ação do proporcional
(ganho Kp=3) que só iria ocorrer no tempo 5 segundos depois. Se não existisse a
ação derivativa, a saída do controlador só seria igual a 15% após 5 segundos.
Entretanto com o tempo derivativo (5 segundos), a saída do controlador já é
igual a 15 % no tempo zero, assim que o controlador calcula a derivada do erro.
Fonte: CAMPOS. 2010. pg. 30
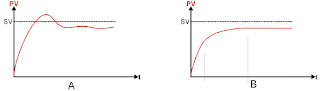
A figura 09 compara respostas hipotéticas de um processo com
controle P e PD. No controle
P (figura 09A), devido à banda proporcional pequena observa-se a presença de overshoot (PV ultrapassa SP antes de
estabilizar). Isso ocorre pelo longo tempo em que MV esteve no seu valor máximo e por ter sua
redução iniciada já muito próximo de SP, quando já é tarde para impedir o overshoot. No controle com ação
derivativa (figura 09B) MV diminui se PV cresce muito rápido, ao antecipar a
variação de PV, a ação derivativa reduz ou elimina o overshoot e as oscilações no período.
Fonte: NOVUS. 2003. pg 05
Ao incorporar um caráter antecipatório à ação de controle, o
modo derivativo tende a estabilizar o sistema. O controle derivativo também
tende a diminuir o erro estacionário porque é possível trabalhar com valores
mais elevados do ganho. Além disso, normalmente melhora a resposta dinâmica do
sistema, diminuindo o tempo de acomodação. (OGATA, 2003, pg. 234)
1.4 Controlador proporcional, integral e derivativo (PID)
É o mais sofisticado tipo de controle utilizado em sistemas
de malha fechada. Trata-se da combinação das ações proporcional, integral e
derivativa para gerar um só sinal de controle dando origem ao chamado
controlador Proporcional Integral Derivativo ou simplesmente PID. (CAMPOS,
2010, pg 29)
O objetivo é utilizar as características particulares de cada
uma destas ações obtendo-se uma melhora significativa do comportamento
transitório e em regime permanente do sistema controlado.
Resumidamente a ação proporcional elimina as oscilações, a
integral elimina o desvio de off-set, enquanto a derivativa fornece ao sistema
uma ação antecipada evitando previamente que o desvio se torne maior quando o
processo se caracteriza por ter uma correção lenta comparada com a velocidade
do desvio (por exemplo, alguns controles de temperatura). (RIBEIRO, 2005,
pg.72)
O sinal de controle gerado (u(t)) pelo controlador PID é dado
como:
Sendo sua função de transferência dada por:
Esta equação expressa o algoritmo de saída do
controlador PID paralelo clássico, sendo este o mais encontrado na prática. Ele
é dito paralelo porque as suas ações, proporcional (P), integral (I) e
derivativa (D) são calculadas em paralelo e em seguida somadas, originando o
sinal de saída.
Fonte: CAMPOS. 2010. pg.
31
Utilizando-se desta combinação têm-se três parâmetros de
sintonia do controlador: o ganho proporcional Kp (ação proporcional), o tempo
integral Ti (ação integral) e o tempo derivativo Td (ação derivativa).
Nem sempre, no entanto, faz-se necessário ou é possível o uso das três
ações de controle para controle de variáveis em processos. Pois cada qual
possui suas limitações perante de terminadas situações. (OGATA, 2003, pg. 557)
A
figura 11 ilustra o efeito da ação do controle PID sob uma variável de um
processo industrial, lembrando de que as variáveis do controle (Kp, Ti e Td)
devem ser ajustadas para que se obtenha uma resposta satisfatória.
Fonte: NOVUS. 2003. pg 6
Escrito por: Fabricio Marqui Sanches Eng. Mecatrônico